Resonance and spectral properties of different quantum models

The project focuses on several issues within the sphere of spectral theory, mainly on resonance and spectral properties of different quantum models. It describes mainly asymptotic properties of Laplace operators and wave operators appearing on graphs. During the project period, the properties of quantum graphs and damped wave equations were investigated. These models describe large classes of mesoscopic systems, like electron behaviour in nanotubes, waveguides, and crystals; fother applications also concern quantum chemistry, optics, and studies of microwave systems. The asymptotic behaviour of the eigenvalues and their statistics plays an important role in quantum chaology.

Damped Wave Equation on Graphs

The project studied several issues from the sphere of spectral theory. In the paper by P. Freitas and J. Lipovsky called: Eigenvalue asymptotics for the damped wave equation on metric graphs, J. Diff. Eq. 263 (2017), 2780–2811

the linear damped wave equation

∂_tt w_j(t,x) + 2a_j(x) ∂_t w_j(t,x) = ∂_xx w_j(t,x) + b_j(x) w_j(t,x),

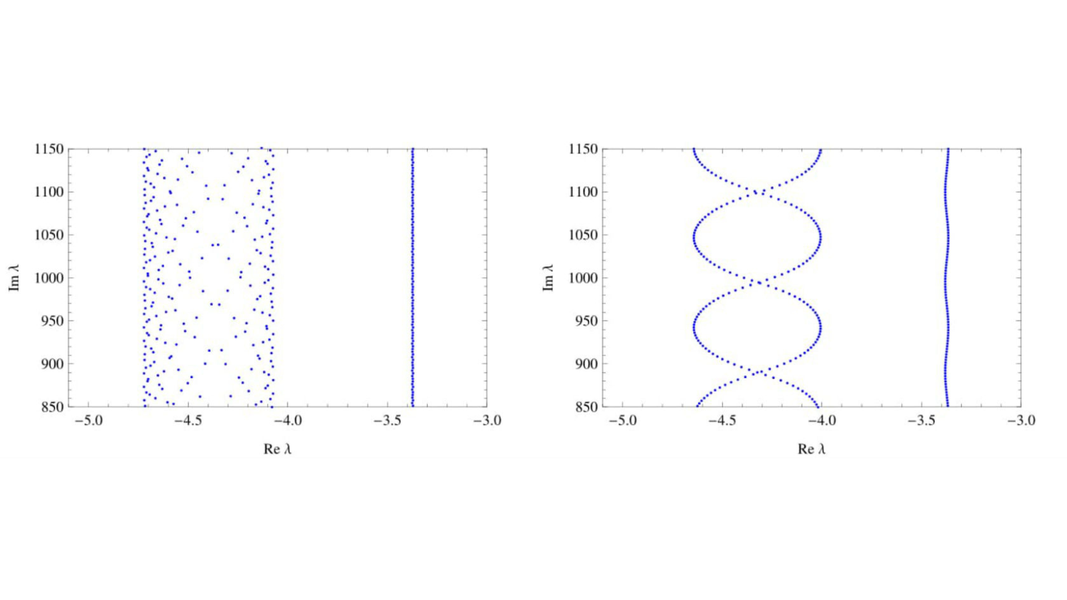
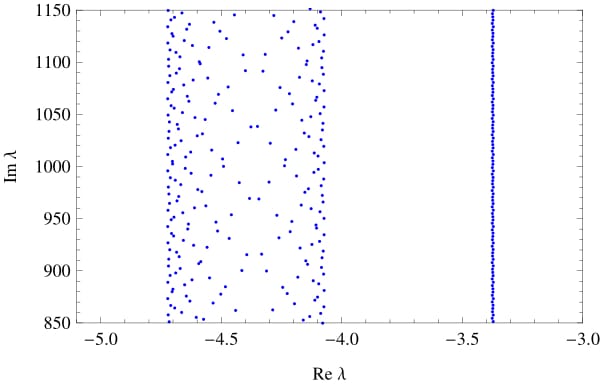
was considered on a finite metric graph, where aj is the damping function, and bj is the potential on the j-th edge. Interesting results were found on the spectrum of the corresponding operator. The issue was previously studied on a segment and on a manifold, but the metric graph provides an interesting intermediate case between a segment and a manifold.

We found that for an equilateral graph (a graph with the same lengths of the edges) sequences of eigenvalues are formed, with their real parts converging to a certain number as their imaginary parts going to infinity. We decided to call these numbers as high-frequency abscissas. We found upper and lower bounds on the number of high-frequency abscissas depending on the number of edges of an equilateral graph and its structure.

Spectrum of a certain equilateral graph with 5 edges.

If the ratio of the lengths of the edges is irrational, the number of high-frequency abscissas can go to infinity.


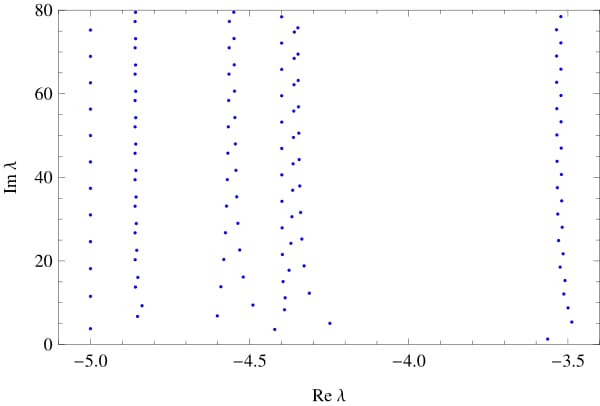
Spectrum of a star graph with different lengths of the edges, l₁ = 1, l₂ = 1, l₃ = 1.03.

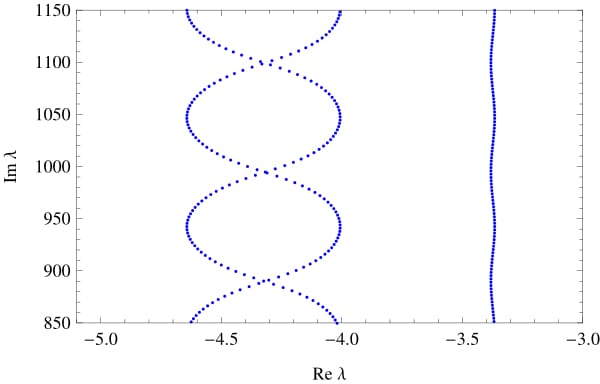
Spectrum of a star graph with different lengths of the edges, l₁ = 1, l₂ = 1, l₃ = 1.41.

Quantum Graphs

In another paper: Pseudo-orbit approach to trajectories of resonances in quantum graphs with general vertex coupling: Fermi rule and high-energy asymptotics, J. Math. Phys. 58 (2017), 042101,
the authors, P. Exner, J. Lipovsky, studied a quantum graph (a metric graph with finite and semi-infinite edges equipped with an operator acting as the negative second derivative with a suitable domain given by the coupling conditions at the vertices of the graph). For this quantum graph the notion of resolvent resonances can be defined as the complex numbers for which there are generalized eigenfunctions with only the outgoing wave on the semi-infinite edges (e.g. the radiation condition f(x) = f(0) e^ikx). Square roots of these resonances are either in the lower complex plane or on the imaginary axis.

Let us consider that for some lengths of the edges the graph has an eigenvalue k₀². If we change the lengths of the edges l_j(t) depending on the parameter t, the eigenvalue may become a resonance k². We computed the second derivative of imaginary part of k with respect to t (which is connected to one of the formulations of the Fermi's golden rule) and also the first and second derivative of the real part of k with respect to t. This allows us to approximate the trajectory of the resonance in the complex plane as t changes.


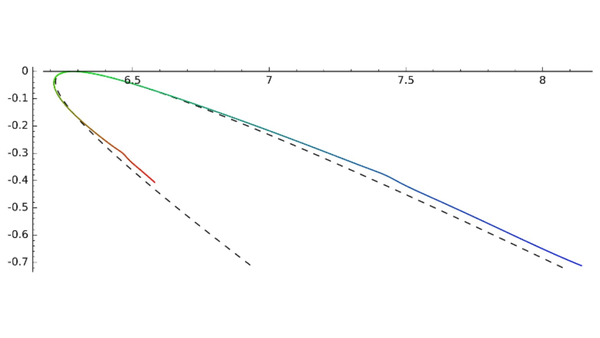
The trajectory of the resonance for a particular graph (dependence of the imaginary part of k on the real part of k); the value of t is denoted by the colour of the curve. The approximation is shown by the dashed curve.